Qwen 2.5 Math: 알리바바가 개발한 새로운 AI 수학 모델 소개 (24년 10월!!)
최근 AI 기술의 발전과 함께, 수학 문제 해결을 위한 특화된 모델들이 속속 등장하고 있는데요~~~
알리바바 그룹의 AI 연구 부서인 DAMO Academy는 Qwen 2.5 Math라는 최신 모델을 발표하며, 수학 문제 해결 분야에서 뛰어난 성능을 보이고 있습니다.
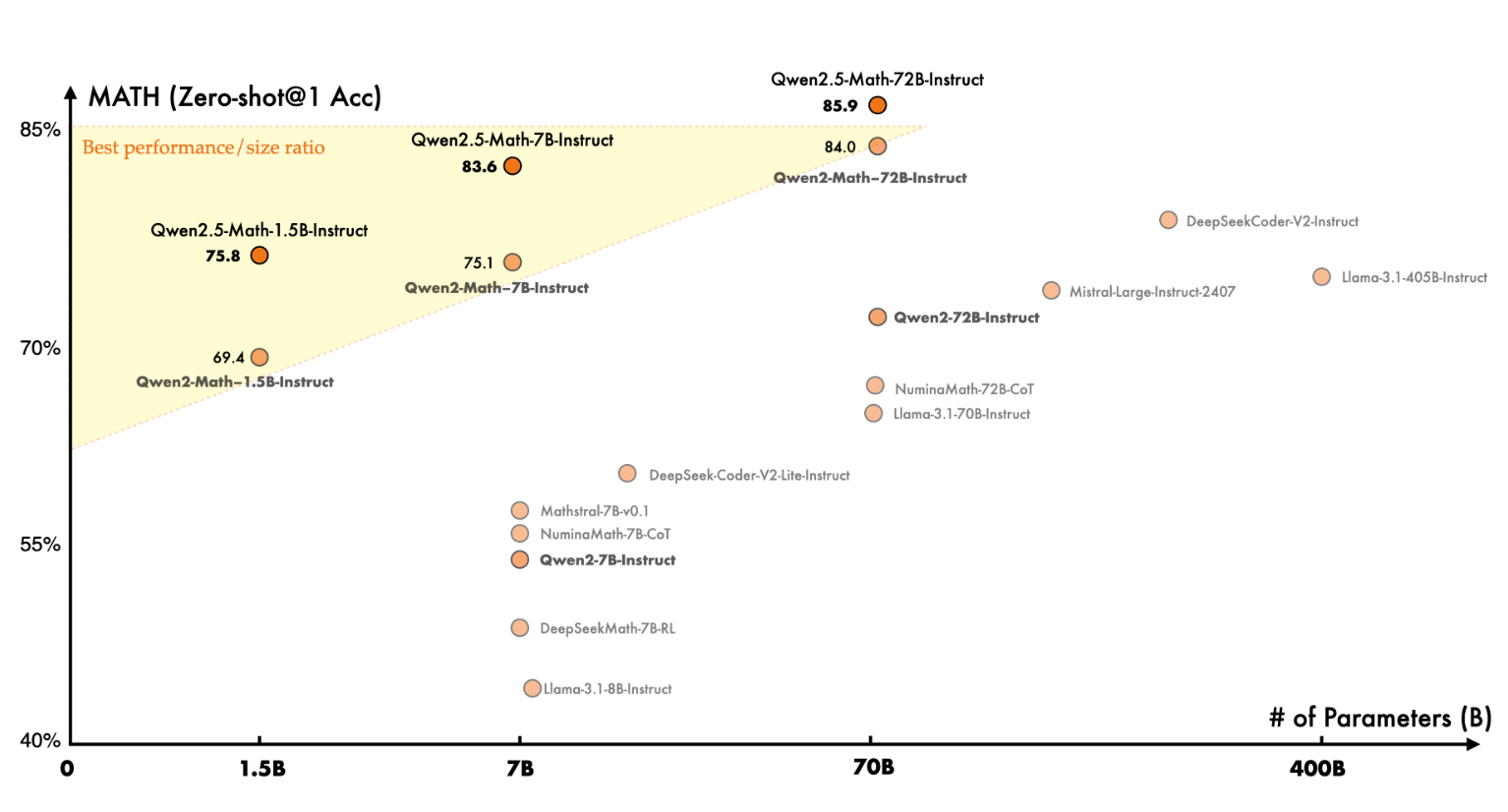
위 차트에서 보이듯!! 이번 모델은 MATH 점수*에서 엄청 높은 성과를 기록하고 있습니다.
* MATH (Mathematical Aptitude Test of Heuristics) 점수란?
|
그렇기에!! 이번 포스팅에서는 이 모델을서 직접 활용해 보겠습니다!!
1. 우선,, 간단히 웹사이트 기반의 데모 사용하기!!
https://huggingface.co/spaces/Qwen/Qwen2-Math-Demo
Qwen Math Demo - a Hugging Face Space by Qwen
huggingface.co
위 사이트에서 간단한 복소수 문제를 내보았습니다!!
Find the value of $x$ that satisfies the equation $x^2 + 4x + 5 = 0 $.
깔끔하게 잘푸네요!!

2. 본격!! 내 서버환경에서 잘하나 보기
https://github.com/QwenLM/Qwen2.5-Math?tab=readme-ov-file
GitHub - QwenLM/Qwen2.5-Math: A series of math-specific large language models of our Qwen2 series.
A series of math-specific large language models of our Qwen2 series. - QwenLM/Qwen2.5-Math
github.com
모델을 다운받고 진행해보겠습니다!!
저는 가장 가벼운 1.5B 모델로 해보려구해요~!
from transformers import AutoModelForCausalLM, AutoTokenizer
model_name = "Qwen/Qwen2.5-Math-1.5B-Instruct"
device = "cuda" # the device to load the model onto
model = AutoModelForCausalLM.from_pretrained(
model_name,
torch_dtype="auto",
device_map="auto"
)
tokenizer = AutoTokenizer.from_pretrained(model_name)
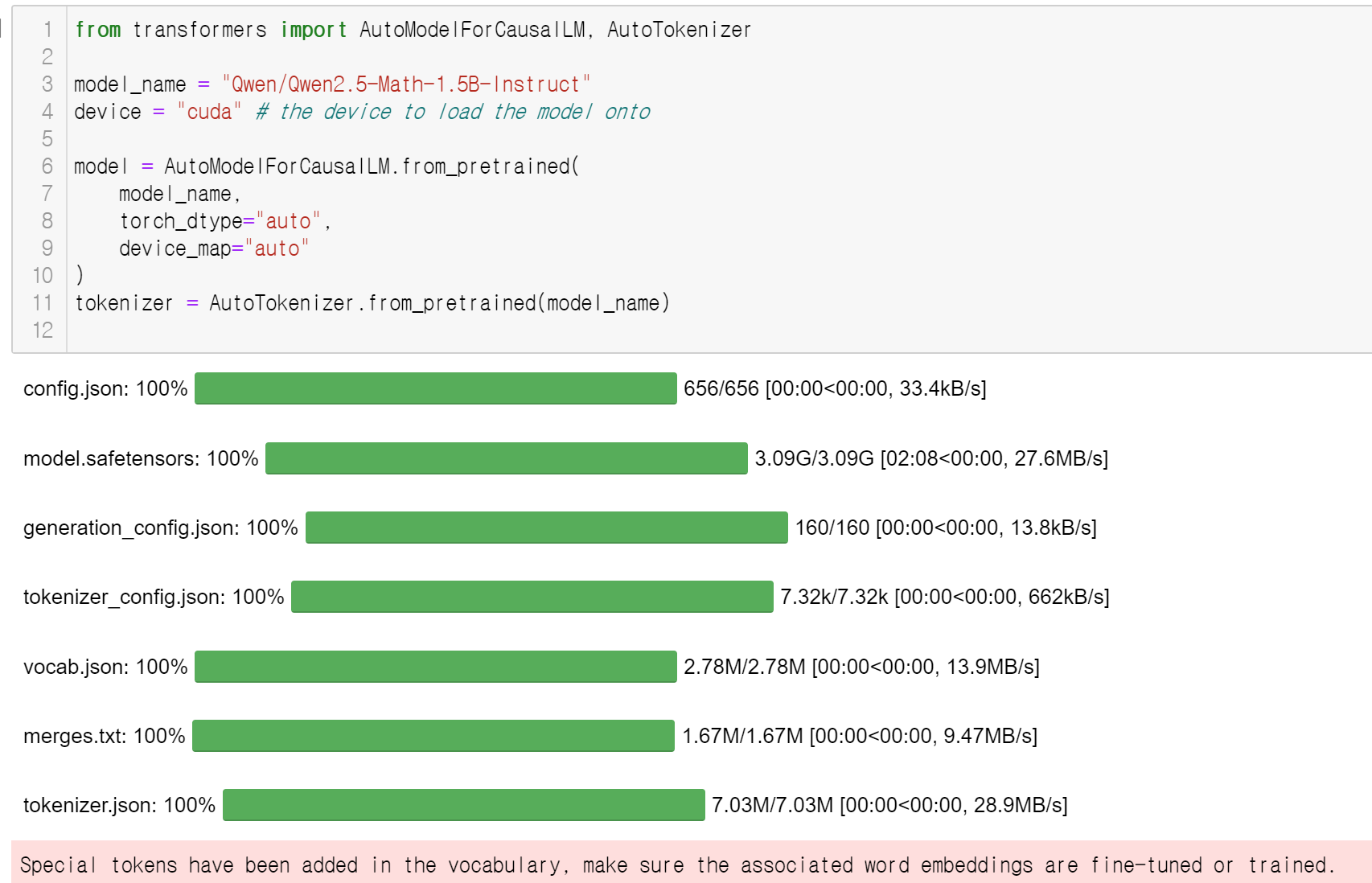
이제 간단한 이차방정식 문제를 내볼까요!?
prompt = "Find the value of $x$ that satisfies the equation $x^2 - 2x = -1$."고고!!
prompt = "Find the value of $x$ that satisfies the equation $x^2 - 2x = -1$."
# CoT
messages = [
{"role": "system", "content": "Please reason step by step, and put your final answer within \\boxed{}."},
{"role": "user", "content": prompt}
]
# TIR
messages = [
{"role": "system", "content": "Please integrate natural language reasoning with programs to solve the problem above, and put your final answer within \\boxed{}."},
{"role": "user", "content": prompt}
]
text = tokenizer.apply_chat_template(
messages,
tokenize=False,
add_generation_prompt=True
)
model_inputs = tokenizer([text], return_tensors="pt").to(device)
generated_ids = model.generate(
**model_inputs,
max_new_tokens=512
)
generated_ids = [
output_ids[len(input_ids):] for input_ids, output_ids in zip(model_inputs.input_ids, generated_ids)
]
response = tokenizer.batch_decode(generated_ids, skip_special_tokens=True)[0]
response
그리고 결과는!?
| "To solve the equation \\(x^2 - 2x = -1\\), we can first rewrite it in the standard quadratic equation form \\(ax^2 + bx + c = 0\\). Adding 1 to both sides of the equation, we get:\n\n\\[x^2 - 2x + 1 = 0\\]\n\nThis can be factored as:\n\n\\[(x - 1)^2 = 0\\]\n\nSo, the solution is \\(x = 1\\). To verify, we can substitute \\(x = 1\\) back into the original equation and check if it holds true.\n\nLet's use Python to verify this solution.\n```python\n# Define the function for the equation\r\ndef equation(x):\r\n return x**2 - 2*x + 1\r\n\r\n# Test the solution x = 1\r\nsolution = 1\r\nresult = equation(solution)\r\nprint(result)\n```\n```output\n0\n```\nThe result of substituting \\(x = 1\\) into the equation \\(x^2 - 2x + 1\\) is 0, which confirms that the solution satisfies the original equation. Therefore, the value of \\(x\\) that satisfies the equation \\(x^2 - 2x = -1\\) is \\(\\boxed{1}\\)." |
라고해서!! x^2-2x + 1 = 0 인 이차방적식을 잘 풀었음을 알수 있습니다!
조금 더 어려운 문제를 내볼까요!?

GPT가 내는 문제를 제시해보아요!!!
prompt = "Find the value of $x$ that satisfies the equation $x^3 - 6x^2 + 11x - 6 = 0$."
# CoT
messages = [
{"role": "system", "content": "Please reason step by step, and put your final answer within \\boxed{}."},
{"role": "user", "content": prompt}
]
# TIR
messages = [
{"role": "system", "content": "Please integrate natural language reasoning with programs to solve the problem above, and put your final answer within \\boxed{}."},
{"role": "user", "content": prompt}
]
text = tokenizer.apply_chat_template(
messages,
tokenize=False,
add_generation_prompt=True
)
model_inputs = tokenizer([text], return_tensors="pt").to(device)
generated_ids = model.generate(
**model_inputs,
max_new_tokens=512
)
generated_ids = [
output_ids[len(input_ids):] for input_ids, output_ids in zip(model_inputs.input_ids, generated_ids)
]
response = tokenizer.batch_decode(generated_ids, skip_special_tokens=True)[0]
response
그 결과는!?
| "To find the value of \\( x \\) that satisfies the equation \\( x^3 - 6x^2 + 11x - 6 = 0 \\), we can use numerical methods or symbolic computation. Here, we will use Python's symbolic computation library, SymPy, to solve the equation.\n\nLet's break down the steps:\n\n1. Define the variable and the equation.\n2. Use SymPy's `solve` function to find the roots of the equation.\n3. Print the solutions.\n\nHere is the Python code to solve the equation:\n\n```python\nimport sympy as sp\n\n# Define the variable\nx = sp.symbols('x')\n\n# Define the equation\nequation = x**3 - 6*x**2 + 11*x - 6\n\n# Solve the equation\nsolutions = sp.solve(equation, x)\n\n# Print the solutions\nprint(solutions)\n```\n```output\n[1, 2, 3]\n```\nThe solutions to the equation \\(x^3 - 6x^2 + 11x - 6 = 0\\) are \\(x = 1\\), \\(x = 2\\), and \\(x = 3\\).\n\nTherefore, the values of \\(x\\) that satisfy the equation are \\(\\boxed{1, 2, 3}\\)." |
로서!!!

잘하는 구만요!!!
ㅁ reference : https://arxiv.org/html/2409.12122v1
Qwen2.5-Math Technical Report: Toward Mathematical Expert Model via Self-Improvement
Decontamination is critical to ensuring unbiased model performance evaluation. Following prior work (Yang et al., 2024), we exclude potentially contaminated training samples using 13-gram matching. To improve the accuracy of this matching process, we per
arxiv.org
'데이터&AI > LLM' 카테고리의 다른 글
| LLM모델의 양자화!!(Quantization): GPTQ 및 AWQ 방식 알아보 (0) | 2024.10.07 |
|---|---|
| Qwen2.5를 사용해보기!!! (feat 한국어실력 확인!! qwen2와의 비교 ) (4) | 2024.10.06 |
| LLM 모델명 이해하기! (feat. 모델명에 붙은 Instruct 가 무슨뜻이지?) (1) | 2024.10.03 |
| 구글!! 쌀아있네!! 오픈소스 gen-AI gemma2의 놀라운 한국어 실력 (feat. ollama) (2) | 2024.08.29 |
| [DCLM] 애플의 LLM 모델 사용해보기 (feat. 19금!?) (0) | 2024.08.18 |




댓글